
Harmonik und Complikation
‚Complikation und Combination‘ als bildende Vorgänge
„Wir geben gern zu, daß sich aus einer Einheit, an einer Einheit ein Diverses entwickeln, eine Differenz entstehen könne; allein es gibt gar verschiedene Arten, wie dieses geschehen mag. Wir wollen hier nur zweier gedenken: Erstens daß ein Gegensatz hervortritt, wodurch die Einheit sich nach zwei Seiten hin manifestirt und da- durch großer Wirkungen fähig wird; zweitens daß die Entwicklung des Unterschiedenen stetig in einer Reihe vorgeht…“ Goethe, Zur Farbenlehre 1810. Polemischer Teil. 1. Buch, 1. Teil, § 27
Farbe, Harmonie und Harmonik
Wenn es um Farbe geht, steht wohl auch heute das Verhältnis der Farben zueinander, der sinnliche Reiz aus entsprechenden Kombinationen, im Mittelpunkt unserer Anschauung und Bewertung. Die farbigen Erscheinungen, aus denen wir im Laufe der Menschheitsentwicklung mehr und mehr die Farbe als eine ‚autonome Größe’ herausgefiltert haben, bieten uns aber eine multidimensionale Mannigfaltigkeit. Sowohl im unmittelbaren Erleben als auch in der Vorstellung erscheint uns jene Mannigfaltigkeit außerordentlich differenziert. Unserem Gesichtsinn wird Farbe ununterbrochen in qualitativer und quantitativer Varianz dargeboten, ist mannigfaltig durch Kontext und Metapher beladen sowie als dynamische Feldgröße unserer Wahrnehmung ständig in Bewegung. So wird Farbe demzufolge auch in mannigfaltiger Weise erlebt und auch heute oft als etwas Flüchtiges und schwer zu Fassendes angesehen. Daraus wird wiederum gern gefolgert, dass objektive Bewertungen schwer fallen oder gar unmöglich oder unzulässig erscheinen. Aber gerade wohl wegen dieser Schwierigkeiten haben sich immer wieder Natur- und Geisteswissenschaftler sowie Künstler daran versucht, die Welt der Farbe zu durchdringen, um Allgemeingültiges auch für unser Verhältnis zur Farbe bzw. für das Verhältnis der Farben zueinander abzuleiten. Auf der langen Liste stehen bekannte Namen wie Goethe, Runge und Schopenhauer, Cheuvreul, Delacroix und Seurat, Helmholtz, Wundt, Hering und Ostwald oder Hölzel, Kandinsky, Itten und Klee so- wie Lohse und Albers. Insbesondere Josef Albers hat mit ‚interction of Color‘ die Relativität der Farbe veranschaulicht.
Hier wird nun kein geschichtlicher Abriss der Farbenharmonielehre gegeben noch eine schlüssige Theorie zur Farbenharmonie vorgestellt. Für Ersteres -die Geschichte- verweise ich aber gern auf die Arbeit von Andreas Schwarz ‚Die Lehren von der Farbenharmonie‘ (Schwarz 1995/ 98). Schwarz gibt darin einen fundierten, kritischen Überblick der Auffassungen von Pythagoras bis zu Parry Moon und Domina Spencer, die 1944 mit ihren Arbeiten auf der Basis des ‚ästhetischen Maßes’ von Birkhoff M = O/C (1933) versuchten, an das pythagoräische Denken mathematischer Begründung anzuknüpfen.
Was eine aktuelle, schlüssige Theorie zu den Farbharmonien angeht, sieht es leider schwieriger aus. Obwohl sich erst 2006 eine Internationale Farbkonferenz in Budapest der Sache wieder verdienstvoll annahm, offenbarten sich auch hier die Schwierigkeiten, das Problem einer elementarästhetischen Bewertung von Farbzusammenhängen fundiert zu ergründen und einer allgemeinen Theorie zuzuführen. Der spiritus rector der Konferenz, Antal Nemcsisc, stellte bereits 1993 mit seinem Buch „Farbenlehre und Farbendynamik“ eine umwelttheoretische Konzeption der Farbenharmonie vor, die von Präferenzuntersuchungen ausging und die außer- ordentlich komplexen Bedingungen des Harmonieerlebnisses untersucht.
Schließlich soll hier der anregende Rück- griff auf Ausgangspositionen der ‚Vorschule der Ästhetik’ Gustav Theodor Fechners von 1876, den der Farbtrendforschers Axel Venn mit Erich Küthe anschaulich in ‚Marketing mit Farben’ ausgebaut und durch einen Überblick über gegenwärtige Tendenzen der Farbforschung ergänzt hat, Erwähnung finden (Küthe/Venn 1995).
Als weiterhin aber wohl geltende Anforderung formulierte Schwarz (1995/98): „Zusammenfassend bleibt festzuhalten, dass die verschiedenenen Mittel und Methoden, mit denen die harmonischen Beziehungen der Farben erfasst werden, die Grundlage und das Kernstück einer jeden Farbenharmonielehre bilden. Durch sie kann die Farbenharmonielehre als exakte Wissenschaft betrieben werden, deren objektiver Charakter durch die enge Beziehung zur Naturwissenschaft in vielen Fällen noch hatte, was in meiner Überzeugung feststand, ehe ich die harmonische Schrift des Ptolomäus gelesen hatte, ….das habe ich also nach Erledigung meiner astronomischen Aufgabe endlich ans Licht gebracht.“ (Kepler 1619)

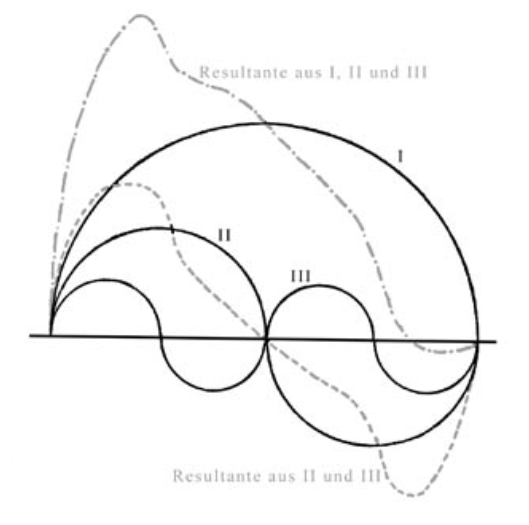
Im vergangenen Jahrhundert erhielt die Harmonik als Lehre neuen Auftrieb durch Untersuchungen von Albert v. Thimus, Hans Kayser, Rudolf Haase u.a. und konnte zeigen, daß die menschliche Natur über „psychophysische Disponiertheiten“ verfügt, die das Verhältnis von Maß und Wert bestimmen und bewerten. So zeigen sich unsere Sinne beispielsweise aufgeschlossen für die Ganzzahligkeit von Intervallen, für Konsonanz-Dissonanz-Unterscheidungen sowie für Diatonik und Chromatik, eine 7- bzw. 12-Stufigkeit von Tonstrukturen.
Eine harmonikale Grundlegung der Farbforschung könnte theoretisch und methodisch befördern, neue Aufschlüsse auch über unser problematisches, stets subjektiv durch Apperzeption überlagertes Verhältnis zur Reihe der Anmutungsqualitäten einschließlich des ‚Harmonischen’, zu gewinnen. Ausgehend vom Gesetz der ‚Complikation‘, welches als allgemeingültiges, natürliches Erscheinungs- und Bildungsprinzip vom Kristallographen Victor Goldschmidt aus der Kristallografie abgeleitet, mathematisch begründet und auf andere Wissensbereiche einschließlich der Farbenlehre übertragen wurde, soll hier der Sachverhalt eines generativen Zusammenhangs der Farbtöne als Grundlegen- des auch für die Harmonielehre abgeleitet werden, wobei es dabei im Besonderen um die Grundlagen der Harmonielehre, die Kombinatorik und Harmonik, geht
Die ‚Complikationstheorie’ und die harmonikale Struktur der Farbe
Zur Farbenlehre. Studienausgabe 2014
Über ein Jahrhundert ist vergangen, seitdem Victor Goldschmidt, Mineraloge und Kristallograph (1853-1933), eigene fundamentale Erkenntnissen aus der Mineralogie mit jener Wissenschaft verknüpfte,
die wir Farbenlehre nennen (GS. 1901) Und obschon dies in der Folge nur wenig Beachtung fand, sollte es uns angesichts veränderter Wissenschafts-Paradigmen aber heute stärker interessieren. Dies um so mehr, weil Goldschmidts Überlegungen einerseits überkommenen, altehrwürdigen Erkenntnissen der Kombinatorik entsprechen, andererseits aber auch weil es scheint, daß sie neuere Erkenntnisse ins- besondere der fraktalen Geometrie bereits vorweggenommen haben.
Goldschmidt hatte zunächst in Untersuchungen über die Entwicklung der Kristall- formen (GS. 1897) ein Erscheinungs- und Bildungsprinzip gefunden, welches er fortan ‚Complikation‘ nennt und später eingehend mathematisch begründet (GS. 1921). Durch Nachweis des Complikationsprinzips auch auf anderen Gebieten gewinnt er erkenntnistheoretisch eine neue Dimension und gelangt zur Überzeugung, daß es sich hier um ein allgemeingültiges Gesetz für die Entwicklung des Mannigfaltigen aus dem Einfachen handeln müsse.
Im Folgenden geht es um die Frage, inwieweit bestimmte Erscheinungs- und Bildungsgesetze, wie das der ‚Complikation’ sowie der damit eng verknüpften ‚Furkation’ und ‚Combination‘ auch für Phänomene der Farbe beansprucht werden können. Goldschmidt selbst hat dazu spezifische Aussagen gemacht, die umrissen werden sollen. Umfassend darauf einzugehen bzw. die Fragestellung hier erschöpfend zu behandeln, erlaubt die große Spannweite farbentheoretischer Aspekte nicht; so sollen nur einige angesprochen und weiterführend Hinweise gegeben werden. Dies betrifft im Besonderen neuere Untersuchungen zur generativen Struktur der Farbtöne.
Eine Relevanz der von Goldschmidt angesprochenen allgemeinen Erscheinungs- und Bildungsprinzipien auch für die Farbentheorie läßt sich naturgemäß am ‚generativen Aspekt‘ der Farbton-Mannigfaltigkeit überprüfen. Dabei interessiert das Generative der Farbtöne sowohl in erscheinungsspezifischer als auch mathematisch ordnungswissenschaftlicher und erkenntnistheoretischer Hinsicht.
Zum Begriff ‚Complikation‘
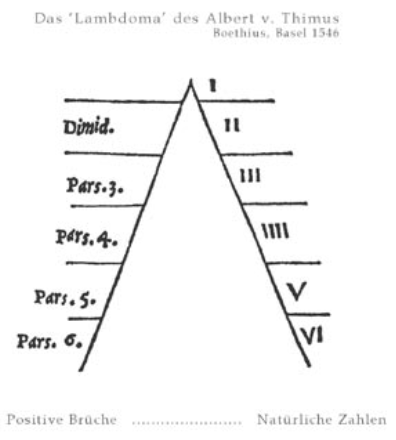
Unter ‚Complikation‘ versteht Goldschmidt die Entwicklung vom Einfachen zum Komplizierten, wofür man in der organischen Natur allgemein den Begriff der ‚Differenzierung‘ hat. Mit Rücksicht aber auf die feste Bedeutung dieses Begriffes in der Mathematik wählt er für seine speziellen Absichten das Wort ‚Complikation‘. Nach GS. erwächst Complikation aus dem Zusammenwirken von Spaltung (Division) und Zusammenlegung (Addition). In Wiederholung vermehrt sich dabei die Mannigfaltigkeit hinsichtlich der Kräfte und Richtungen. Innerhalb linearer Strecken fester Begrenzung (0…∞) kommt es zu symmetrischer ‚Knotenbildung‘. Durch die Lage der Knoten entstehen in Bezug auf die Gesamtstrecke in sich symmetrische Verhältnisse, welche in Zahlen ausgedrückt eine reziprok gestaffelte sog. ‚harmonische Zahlenreihe‘, und wenn diese lückenlos erscheint, eine sog. ‚Normalreihe‘ bilden (Abb. I.1.05). ‚Complikation im engeren Sinne‘ seien die ‚Halbierung‘ (als einfachste Teilung) und die ‚Vereinigung von je einem Teil‘ (als einfachste Addition).
Stärke, Wahrscheinlichkeit, Endlichkeit
Von den abgeleiteten (eingeschobenen) Kräften sei die erste Implikation (Einschiebung) die wichtigste. Sie wird als ‚Dominante‘ bezeichnet. Nach dem Gesetz der ‚Descrendenz‘ nimmt die Stärke der eingeschobenen Glieder gegenüber den Ausgangsgliedern ab. Von der Stärke der eingeschobenen Vektoren hängt ihre Wahrscheinlichkeit ab. Sinkt diese unter eine bestimmte Grenze, so wird sie praktisch, d.h. für die Ausbildung in der Natur, gleich Null. Complikationsreihen können mathematisch allgemein als unendliche konvergente Reihen angesehen werden, von der praktisch nur die ersten abgeleiteten, die stärksten, die wahrscheinlichsten Glieder in Erscheinung treten.
…
Vollständiger Beitrag zum Download:
Verantwortung liegt bei dem Urheber des Beitrags: Eckard Bendin

